Fractal geometry is a branch of mathematics that studies complex shapes and patterns that repeat at every scale. Unlike traditional geometry, which deals with smooth shapes like circles and squares, fractals are often irregular and fragmented. Examples include:
Fractal geometry helps explain natural patterns and is widely used in science, art, and technology.
Here are real-life examples of Fractal geometry
Fractal geometry helps explain the self-repeating, complex patterns in nature and is used in various scientific and engineering fields.
Fractal geometry plays a significant role in architecture, especially in traditional and religious structures. Here are examples:
Fractal geometry adds visual harmony and complexity to architectural designs across cultures, blending art and mathematics.
Fractal geometry is a fascinating branch of mathematics that explores complex shapes and patterns found both in nature and in mathematical constructs. Unlike traditional Euclidean geometry, which focuses on simple shapes like lines, circles, and squares, fractal geometry deals with shapes that exhibit self-similarity and intricate patterns at every scale. These shapes are not just theoretical but can be seen in natural systems such as trees, coastlines, and even clouds.
Fractals may seem like a modern concept, but the idea of self-similar patterns has been around for centuries. Early discussions of fractal-like structures date back to the work of mathematicians like Georg Cantor and Helge von Koch in the late 19th and early 20th centuries. However, it wasn’t until Benoit Mandelbrot introduced the term "fractal" in the 1970s that the field truly began to take shape.
At its core, a fractal is a shape or pattern that exhibits self-similarity—meaning the shape looks similar, no matter the scale at which it is viewed. This unique property allows fractals to be infinitely complex while still maintaining a clear structure.
One of the most important aspects of fractals is that they are recursive, which means they are built by repeating a simple process over and over again. This recursive nature is what makes fractals appear endlessly intricate, even though the rule governing their creation is simple.
Mathematical Foundations of Fractals
Fractal geometry is built on mathematical principles that revolve around recursion, iteration, and the concept of scaling. At the heart of fractal creation is a simple equation or algorithm that is repeated multiple times to generate complex structures. This process, known as iteration, is central to understanding how fractals are formed.
One of the most famous examples of fractal geometry is the Mandelbrot Set, named after Benoit Mandelbrot, who discovered it in the 1970s. The Mandelbrot Set is a set of complex numbers that produces a stunningly intricate fractal when graphed. Its boundary exhibits infinite detail, with smaller versions of the overall set appearing within itself—a hallmark of fractal structures.
Fractal geometry extends far beyond mathematics, finding applications in various fields such as computer graphics, economics, and biology. In computer graphics, for example, fractals are used to create realistic landscapes, textures, and patterns that would be difficult to model using traditional geometry.
In economics, fractal geometry helps analyze market fluctuations, where stock prices exhibit fractal-like patterns. This has led to new models that more accurately reflect the unpredictable nature of financial markets.
The use of fractals in computer graphics is one of the most visible applications of this geometry. By applying fractal algorithms, designers can generate highly realistic textures and natural scenery, such as forests, clouds, and mountain ranges. The ability of fractals to produce organic, lifelike patterns makes them invaluable in fields like video game design and film production.
The financial markets are notoriously unpredictable, but fractal geometry offers a new way to analyze market behavior. Stock prices often follow patterns that resemble fractals, with short-term fluctuations mimicking longer-term trends. This self-similar behavior can help economists and financial analysts model risk and understand market volatility in a more comprehensive manner.
Fractal geometry is closely tied to chaos theory, a field of study that deals with systems that are highly sensitive to initial conditions. Many chaotic systems, such as weather patterns and fluid dynamics, exhibit fractal behavior. Fractals provide a framework for understanding the seemingly random, yet patterned, nature of chaotic systems.
Natural systems, from the formation of clouds to the branching of rivers, often display chaotic behavior that can be modeled using fractals. These systems are unpredictable in the short term but exhibit a long-term pattern that can be understood through fractal analysis. This connection between chaos and fractals has opened up new ways to study complex, dynamic systems.
One of the key challenges in fractal geometry is how to measure the complexity of fractal shapes. Traditional measurements like length, area, and volume don’t work well for fractals, as their complexity increases with each level of magnification. Instead, mathematicians use specialized methods like the fractal dimension to quantify this complexity.
What do seashells, hurricanes, snowflakes, the structure of human lungs and the built Kandariya Mahadev temple in Khajuraho have in common?
They are examples of fractal geometry in nature and its use by humans. Fractal geometry is a branch of mathematics that studies shapes and patterns exhibiting self-similarity and complexity across different scales. It explores irregular and fragmented natural shapes, such as coastlines, mountains, clouds, and plants. Its application in real life varies from identifying irregular heartbeat patterns and detecting tumors in the human body to architecture and designing antennas.
Seashells exhibit fractal patterns in their spirals and overall structure, showcasing natural self-similarity and complexity.
Hurricanes display fractal geometry in their swirling patterns, demonstrating the scale-invariance of natural phenomena.
Each snowflake has a unique fractal design, illustrating the infinite variability and self-similarity of natural structures.
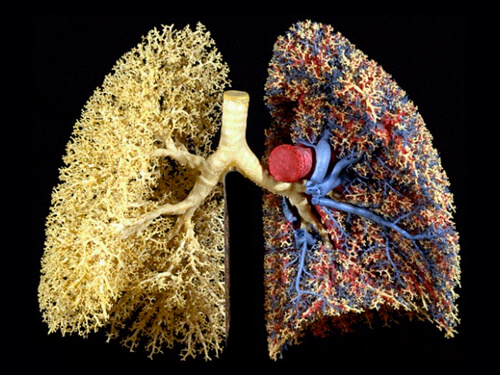
The branching pattern of human lungs follows fractal geometry, optimizing surface area for gas exchange.
This temple in Khajuraho features fractal architectural elements, demonstrating the application of fractal principles in human design.
Euclidean geometry explores objects and their juxtaposition as 0-D for points, 1-D for straight lines, 2-D for planes, and 3-D for volumetric objects like cubes and spheres. “Fractal” objects have an intermediate dimensionality, such as 1.6 for an irregular line or 2.4 for an image “surface”. Generally, the higher the fractal dimension, the finer and “rougher” the texture. Also, fractal objects are self-similar, that is, no matter what scale you measure the object by, statistically, it will be the same. That is, the logarithm of the measured perimeter will obey a linear relationship to the logarithm of the ruler length.
The fractal dimension (D) is often a non-integer which reflects the fractal’s complexity. The D also provides a measure of how the fractal pattern changes. The Coastline Paradox was first observed by Lewis Richardson. He observed that measuring the length of a coastline changes with the scale of measurement due to its fractal nature.
Several methods can be used to calculate fractal dimensions, each suitable for different types of fractals. Here are the most commonly used methods:
There is another application of the box-counting method called the Minkowski-Bouligand dimension.
The Hausdorff dimension is a more rigorous concept that covers the fractal with sets of varying sizes and calculates the limit of the sum of the diameters raised to dimension d.
In nature, fractals are seen as spirals or branching patterns. They appear on trees, river streams, ferns, brain neurons, blood vessels in the lungs, and lightning bolts. The Fibonacci sequence is a natural representation of the fractal dimension and is often referred to as the Golden Ratio which occurs in nature. It appears in the spirals of the sunflower, broccoli, nautilus shell, galaxy, and human body. Another example of the fractal dimensions is Barnsley’s Fern, a formula applied to produce unique fern-shaped objects. Barnsley’s Fern is based on the theory that fern patterns can be mathematically generated and reproduced at any magnification or reduction. Even though lightning does not travel in a straight line, the chaotic and jagged path of several miles that it spans in microseconds across a 3D space. Coupled with thunder, which is a fractal sound caused by the superheating of air, the time it takes for us to hear the thunder and observe the lightning varies since it occurs in a fractal pattern.
Fractal geometry has applications in sound engineering, aerospace research, medical sciences, biotechnology, nuclear physics, photography and architecture among many other avenues. Many interesting and complex ideas such as the Butterfly Effect are built around fractal geometry. The theories and measures arising from fractal geometry have wide application and the patterns can be observed everywhere.
The box-counting method is a technique used to measure the fractal dimension of an object by counting how many smaller boxes it occupies.
Fractals are often found in chaotic systems, helping to model unpredictable natural phenomena.
The Mandelbrot Set is a famous fractal that exhibits infinite complexity and self-similar patterns.
Fractals are used to create realistic textures and landscapes in computer-generated imagery.
Yes, fractals are commonly observed in nature, such as in trees, mountains, and rivers.
A fractal is defined by its self-similarity, meaning it looks the same at different scales.
Yes, fractal patterns are found in music compositions, especially in rhythm, melody, and harmony, where repeating patterns occur at different scales.
Fractals are used in computer graphics to create realistic landscapes and textures, like mountains, clouds, and water, by simulating natural, self-repeating patterns.
Yes, fractals are used in both traditional and digital art. Artists like Jackson Pollock unintentionally used fractal patterns in their work, and modern artists use fractals for intricate, self-repeating designs.
The Mandelbrot Set is a famous fractal that displays infinite complexity. When zoomed in, new, self-similar shapes continuously appear, illustrating the essence of fractal geometry.
Fractals help model complex systems like weather patterns, where small changes can lead to unpredictable outcomes, similar to how fractals behave in nature.
A fractal is a shape or pattern that repeats itself, no matter how closely you look at it. For example, a tree branch looks like a smaller version of the entire tree. Fractals can be found in nature, art, and even in financial markets.
The golden ratio is not a fractal, but it is related to fractals. The golden ratio is a mathematical constant often seen in nature and art, while fractals are about repeating patterns. Some fractals, like the Fibonacci sequence, incorporate the golden ratio in their structure.
tal Geometry? Fractal geometry studies complex patterns that repeat at every scale. Unlike traditional geometry, fractals involve shapes that are often irregular and infinitely detailed, such as coastlines, mountains, or branching structures like trees.
In trading, fractal patterns are used to predict price movements. These patterns repeat at different time frames, allowing traders to make decisions based on trends visible in both short-term and long-term data.
Fractal geometry is used in finance to model market patterns and price movements, especially in complex systems like stock markets. It helps describe how prices change at various scales, identifying trends and cycles in unpredictable markets.
Unleashing Leadership Potential: How IGCSE and IB Programmes Transform Learners into Leaders
Brochure
© Knowledgeum Academy
